Chapter 5: Strategy
What exactly is a strategy for playing
video poker? A strategy tells you which cards you should keep to give you
the highest return. For every hand that is dealt, an exact expected return can
be calculated for each combination of cards that are held. For example, if you
are dealt a full house, then you could do a number of things such as:





Hold all the cards
Hold
three-of-a-kind
Discard
all the cards
The
correct decision here for 9/6 Jacks or Better is to hold all the cards because
holding all the cards gives you the best “Expected Value” (EV). Expected value
indicates how much you can expect to win, on average, from a given hand. For
example, if you hold 3 of a kind, then sometimes you will end up with 3 of a
kind, sometime you will end up with a full house, and sometimes you will end up
with 4 of a kind. The expected value is the average value given all the possible
draws to a particular hand. Without worrying about the specifics of how this is
calculated, the important thing to know is that you always want to hold the
cards that have the highest EV. In the long run, this will maximize your
reward.
There
will be times when holding the hand with the highest EV will NOT produce the
best outcome. For example, if you
held the three-of-a-kind, hoping to get four-of-a-kind, there would be times
when you would end up with four-of-a-kind (which is better than a full house).
But because there is no way of knowing when you will draw that four-of-a-kind,
your best bet is to keep the full house. So
don’t chastise yourself when you do the right thing and a card appears which
would have given you a better hand if you had done the “wrong” thing. In
the long run, playing hunches (i.e., doing the wrong thing) will cost you
money.
Throughout
this book, pictures have been used extensively to facilitate understanding
of the important concepts of video
poker. We continue this approach by presenting strategy cards in a format that
takes advantage of our powerful ability to use a visual image to understand
complex relationships. These strategy cards offer a fairly radical
alternative to the traditional strategy cards. Specifically, most strategy
cards simply present a list of hands that are ordered by their expected
value. These cards have very little
structure in that a player must know which rules to check. Since there may be
more than 40 rules, then it can be quite frustrating using these cards because
you will have to learn on your own which hands interact with each other.
Instead of a list of expected values, these
cards present a strategy that is both hierarchical and graphical. The strategies are “hierarchical” in that the
rules are broken into groups that facilitate learning and understanding. A
hierarchical procedure is easy to follow because it breaks the process
into steps that can be easily
understood. The graphical nature of the cards makes the interactions between
hands more evident.
But enough
talk, grab the laminated “Jacks or Better” card, and we’ll see how it works.
The goal of the card is to hold the hand with the highest
expected value. We do this by
following the connections on the card and trying to reach the highest point
possible. Starting on side 1, let’s look at the “Pair” box on the far left. If
we do have a pair in the hand we are checking, we then try and improve on upon
that hand by seeing if any connections lead to higher hands that are also
satisfied by the hand we are checking.
For example,
what if we are dealt the following cards?





Here,
we have a pair of fours, but we also have four to the flush (which has a
connection from the “2-10” part of the pair box). The colored lines indicate connections from specific pairs. For
pairs, blue lines connect to hands that need to be checked when you have a pair
of 2-10, red lines connect to hands that need to be checked when you have a
pair of jacks or better. As you can see, there are only a couple of hands that
need to be checked when you have a high pair (e.g. 4 to the straight flush or
royal are the only hands that you would hold instead of a high pair).
Of course, if you
have any pair, but also have two pair (or three of a kind, etc.) then you would
hold the two pair (or three of a kind, etc.). For any pair, you want to follow
the connections up as high as possible. For example, a full house is better
than 3 of a kind because the full house is higher on the card than the 3 of a
kind.
If we do not find a pair, we follow the arrows to the right
and check the next box (which is the flush box). We continue this until we hit a
boxed hand that is satisfied.
If we cannot find a hand in one of the boxes on side 1, we
move to side 2, which is where we check for high cards. High cards
are jacks (J), queens (Q), kings (K) and aces (A). Each number of high cards
(printed in red at the left of the card) has it's own structure. Like side 1,
we try and find connections to higher hands.
The hierarchy is user-friendly because it highlights the
relationships between hands. For example, if we have two high cards,
and they are KJ (and none of the
previous levels of the hierarchy have been satisfied), then we keep them both
unless we also have a Jack-Ten in the same suit. This is so because we can only
go up by our connection from KJ to the suited-JT hand. If we had a queen and a jack and reached
this part of the decision tree, then we would be done (i.e. we would hold the
queen and the jack) because there are no connections up from the queen jack.
In order to use
the strategy, you must become familiar with one concept known as a “gap count”.
The gap count is a way of estimating how good a 3 card straight flush. The
lower the gap count, the better the hand.
Remember that a straight flush is 5 cards that are in order but also in
the same suit (e.g., 5,6,7,8 and 9 of spades). 3 cards to the straight flush is
a decent hand in many video poker games because there are lots of opportunities
for straights, flushes and a slim chance of filling the straight flush. As you
would expect, 3 card straight flushes
that are completely sequential (like the 7, 8, and 9 of spades) are better than
3 card straight flushes that have gaps in the sequence (such as 7, 8, and 10 of
spades).
Every 3 card straight flush has 0, 1, or 2 gaps. A gap is
any hole in the sequence. For example, if you are dealt 5,6 and 9 of spades,
then you have two gaps (because the 7 and 8 are missing). Remember that you can
use an Ace as a low card (Ace, 2, 3, 4 and 5 of the same suit make a straight
flush) or as a high card (10, jack, queen, king and ace of the same suit will
make a royal straight flush). However, any 3 card straight flushes with an Ace
used as a low card automatically become a 2 gap straight flush. Straight
flushes with aces in them can be difficult to catch. Fortunately, if you do
miss these combinations, it will not impact your return in any significant way
(unless you are dealt the straight flush and throw away 250 coins!). As a
precaution, simply check a little extra when you have an Ace and a lot of cards
in the same suit.
To make things a little more complicated, any card in the
straight flush that is a jack or higher adds considerably to the expected
value. This is because a high card may be paired up for Jacks or Better.
Fortunately, the increase in value for a high card is just about the same as
the value of removing a gap in a straight flush. Therefore, you need to
subtract 1 gap for each card that is a jack or higher. Let’s look below at some “gap counts” for
various hands.





This hand has 1 gap (it’s missing the ten of spades), but
it has one high cards. So we start with 1 gap and subtract 1 to get a gap count
of 0.





This hand has 0 gaps, but it has no high cards. So we
start with 0 gaps and subtract 0 to get a gap count of 0.





This hand has 2 gaps, but
it has 1 high card. So we start with 2 gaps and subtract 1 to get a gap count
of 1.




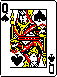
This hand has 2 gaps (it is
missing the 9 and the 10 between the 8 and the jack), but it has 2 high card.
So we start with 2 gaps and subtract 2 to get a gap count of 0.
Consider the following
hand:





This hand has 2 gaps, but with 1 high card (even though
the ace is used as a low card, it is still considered a high card, because you might
pick up a pair of aces, which is why high cards make the hand more valuable).
It appears to have only 1 gap, but since it uses an ace as a low card, but it
really has two gaps because we would need a deuce and a five to fill the
straight or straight flush. Ace, two and three also has two gaps, even though
it appears to have 0 gaps.
Of
course, you might end up with a gap count of -1(with a 9, 10 and jack of a
suit, or a queen, jack and 9 of a suit), but this is pretty rare.
The
strategy cards use some conventions to show different kinds of hands. At the end
of the book, you will find a summary of these codes. This summary page, like
the laminated strategy cards, is printed in colored ink to facilitate
understanding. Don’t worry about memorizing all these codes, we will go through
many sample hands which will help you get used to the codes.
Flush
Combinations are in Blue
Gap counts are
calculated by counting the number of physical gaps and subtracting
the number of high cards. For example,
Q-J-8 in the same suit is 0 gaps (not 2) because, although there are 2 physical
gaps, there are also 2 high cards which produces a gap count of 0 (2-2).
The "/" means “or” in
that "KT/QT" means "Suited king-ten or suited queen-ten"
“H” indicates a
high card (jack, queen, king or ace).
“A(HH)” means keep
the lowest two high cards if dealt AHH where H is jack or
above.
Str
= Straight
Fl
= Flush
SF
= Straight Flush
“Suited
2” means two high cards in the same suit (e.g. Queen and King of hearts).
The
following three chapters describe near-expert strategy for the three most
available and popular video poker games. The
near-expert strategy is described for double bonus because while it is easier
to learn than the complete expert strategy, this near-expert strategy provides
a reward which is very close to the expert strategy (remember the flattening
out of the curve from the introduction?). For “Jacks or Better” or “Deuces
Wild”, only the expert strategy is provided because this strategy is
sufficiently easy to learn.
Now, we can dive into the strategies for the 3 most popular games in the next 3 chapters (Chapters 6-8). If you like, you can jump right to any of the three chapters which describe the strategies for the three most popular video poker games (Jacks or Better, Double Bonus, and Deuces Wild). Some of the information in one chapter may be repeated in the other chapters. While this might be a little redundant, it offers the option of skipping to any of the three chapters.